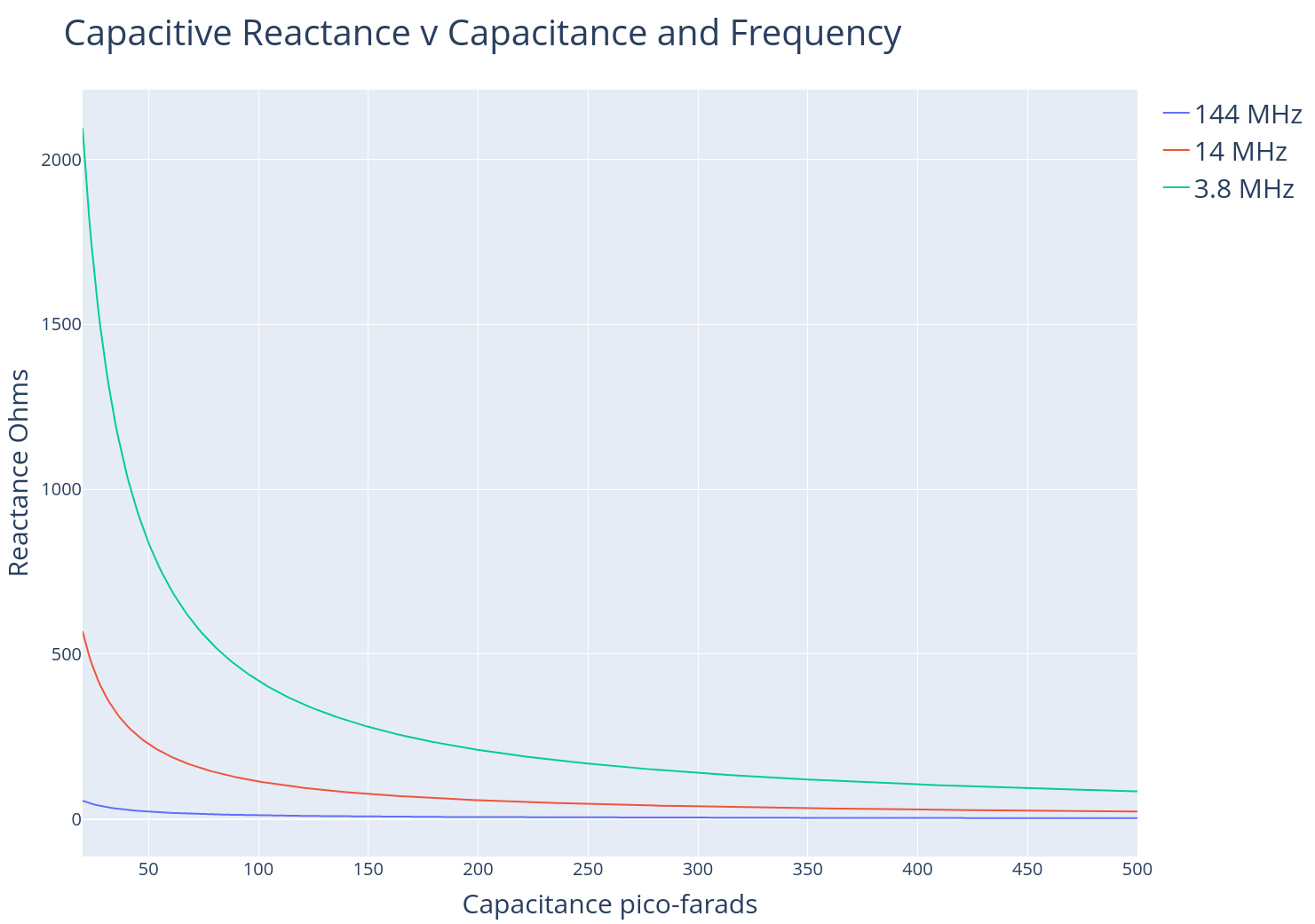
Impedance is the opposition to alternating current presented by the combined effect of resistance and reactance in a circuit. Reactance is the opposition of alternating current in a circuit imposed by a capacitor or inductor. The amount of reactance imposed by a capacitor or inductor depends on the frequency of the alternating current in the circuit. Understanding the relationship of capacitive reactance and inductive reactance is critical to understanding resonance in amateur radio.
\(X_c = \frac{1}{2\pi f C} \)
\(Xc = \text{Capacitor } \text{Reactance } \text{in } \text{Ohms }\\ C = \text{Capacitance in farads} \\ f = \text{Frequency in Hertz}\)
Capacitors store energy in an electric field. So what effect do capacitors have in an AC circuit? According to the equation above, capacitive reactance is inversley proportional to frequency and the value of the capacitor. To put it simply, there will be more resistance to the flow of alternating current for capacitors with smaller values. There will also be more resistance to the flow of alternating current for lower frequencies. For example, there will be more capacitive reactance at a frequency of 3.8 MHz than for a higher frequency of 144 MHz. Larger value capacitors pass AC or radiowaves better than smaller ones. Capacitors with less capacitance in Farads inhibit the flow of AC or radio waves. If you want to attenuate or even block a AC signal, use a small capacitor and lower frequency.

\(X_L =2 \pi f L\)
\(X_L = \text{ Inductive Reactance in Ohms}\\ L = \text{ Inductance in Henries} \\ f = \text{ Frequency in Hertz }\)
Inductors store energy in a magnetic field. Inductors and capacitors are critical elements in radio circuits. Are we starting to understand why radio waves are composed of electro-magnetic energy? Inductive reactance is easier to understand. The reactance imposed by an inductor in an AC circuit is directly proportional to frequency and inductance. Larger value inductors cause greater resistance to the flow of alternating current. Similarly, higher frequencies cause greater opposition to flow of alternating current or increase inductive reactance. If you want to attenuate or block the flow of radiosignals use a higher value inductor or higher frequency.
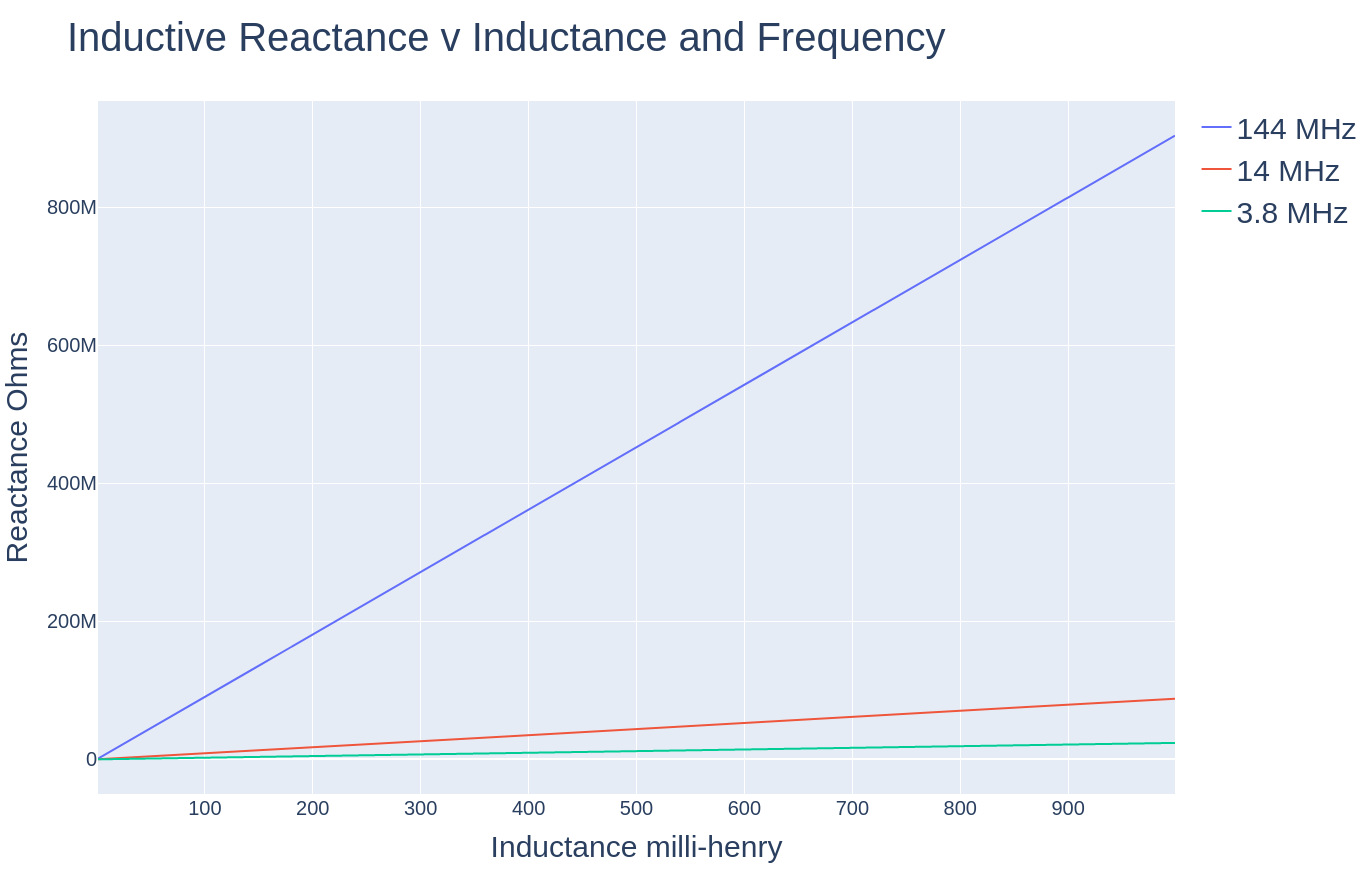
Now that we have defined inductive reactance and capacitive reactance we may derive the formula for resonant frequency based on the equations above. Resonance is achieved when inductive reactance equals capacitive reactance. This is expressed as ...
\(X_L = X_C \\ 2\pi fL= \frac{1}{2\pi f C} \)
Lets solve for Frequency .....
\(f^2 = (\frac{1}{2\pi C}) (\frac{1}{2\pi L})\)
\(f = \sqrt{\frac{1}{4 \pi^2 LC}}\)
\(f = \frac{1}{2 \pi \sqrt{LC}}\)
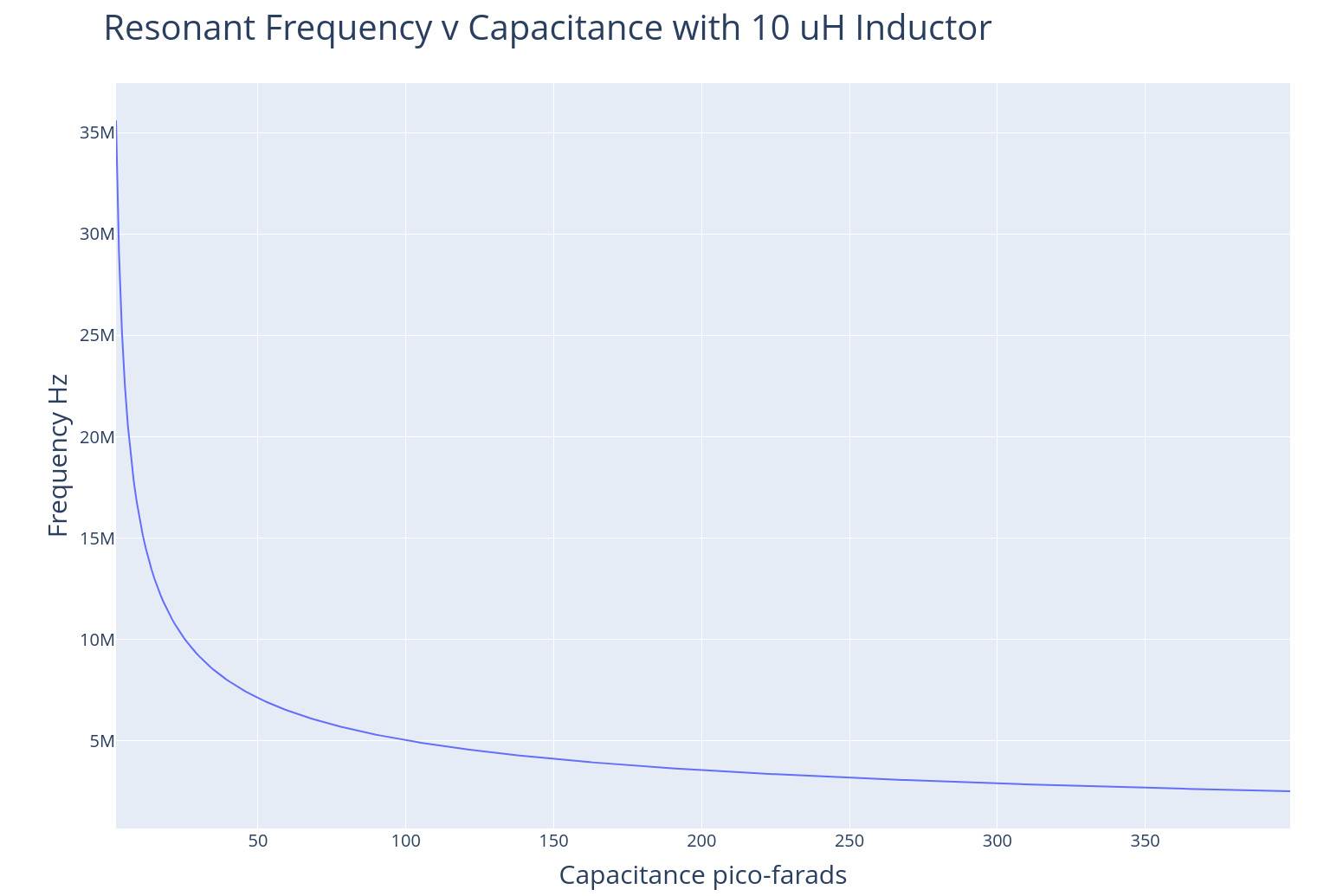
If you know your resonant frequency and your capacitor value you can figure out what size inductor you need.
\(L = (\frac{1}{4 \pi^2 f^2 C})\)
If you know your resonant frequency and your inductor value you can figure out what size capacitor you need.
\(C = (\frac{1}{4 \pi^2 f^2 L})\)